LOST IN QUANTUM CRYPTOGRAPHY

Jun 2025

Álvaro Yángüez Bachiller

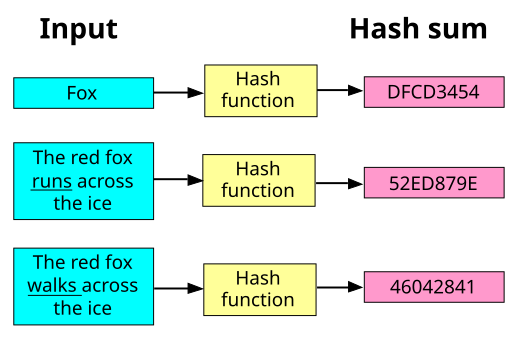
In my last story of the month, we saw how a cryptographer navigates the classical landscape—toggling between symmetric and asymmetric schemes, public-key encryption and key exchange, Minicrypt and Cryptomania. We even discovered that by borrowing quantum subroutines, a task like multiparty computation (MPC), classically doomed to Cryptomania, can descend into Minicrypt. But have we really scratched the surface of what “quantum” means when we wear the lenses of a computationally bounded cryptographer? As it turns out—surprisingly—not at all.

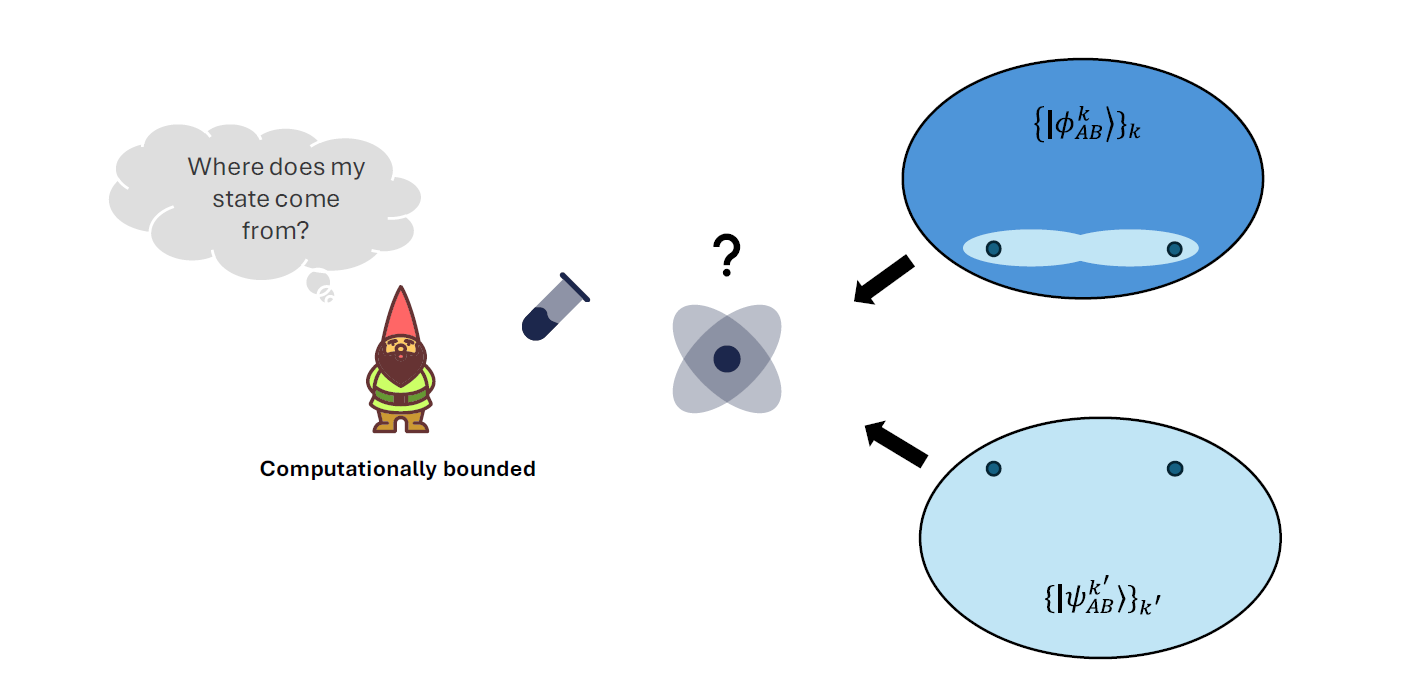
First, let us rewind. What does it mean to be computationally bounded? A malicious adversary might have unlimited power (the so-called information-theoretic or unbounded model), or might be restricted by the limits of efficient computation (the polynomial-time model). In our previous story, we focused on classical restrictions: one-way functions (OWFs) are the minimal assumption for any computational cryptography. If OWFs fail to exist, then classical cryptography crumbles—no digital signatures, no public-key encryption, no MPC from classical means alone.

Once quantum mechanics enters the arena, however, this picture changes dramatically. In 2018, Ji et al. introduced an intrinsically quantum primitive that sits potentially below OWFs in hardness: pseudorandom quantum states (PRS). A PRS is a family of efficiently generated quantum states that, to any polynomial-time quantum adversary, are indistinguishable from truly random states. If you’ve been following the quantum computing headlines, you might be wondering: “Aren’t quantum computers supposed to break everything?” In reality, there will remain problems—especially quantum-native problems—that high-powered quantum machines still cannot solve efficiently. That is precisely where PRS live.

For our beleaguered cryptographer, this is welcome news. Even if classical cryptography evaporates under quantum assault—if OWFs no longer exist or are shattered by a quantum algorithm—we can still build meaningful cryptographic functionality from PRS alone. In other words, quantum cryptography need not collapse simply because classical assumptions succumb to quantum breakthroughs.

Naturally, this breakthrough provokes many new questions—and more work for our cryptographer protagonist. Which classical protocols admit a purely quantum analogue under PRS? Can we identify even weaker quantum assumptions, or new hierarchies of computational worlds? Do Impagliazzo’s original “worlds” split further when quantum resources are allowed, or do entirely new worlds emerger? The answers are far from obvious, and the journey is only beginning.