QKD in practice: Opening the Chamber of Decoy State Secrets

This Story of the Month brings us back in time to a certain school, where a certain person that some of you might find familiar first learned about an incredible wizardry. As every proper story, we shall begin with…

Once upon a time, in a galaxy far, far away, there was a young man called Harry Quanter. Despite people referring to him as a ”sorcerer”, or ”the Chosen One”, Harry was just your ordinary Ph.D. student in Physics with exceptional passion, innate curiosity and a below-average amount of social interactions. One day our protagonist stumbled upon a very interesting tale describing how quantum mechanics (that is, the greatest of magics) could be used to provide secure communication in every realm (you can find this very same tale at https://quantum-safeinternet.com/stories/1615-2/). Fancied by this, he immediately ran to the office of Professor Albus Percival Wulfric Bennett Brassard Scrödingdore, head of the Faculty of Quantum Mechanics and ambiguous cat lover.

We shall report here the enlightening conversation they shared on that day.

H) Professor Scrödingdore! I found out about an incredible technique called Quantum Key Distribution (QKD)!

S) I see you are a man of taste, dear Harry. Indeed, QKD is a promising tool that could allow us to overcome any eavesdropping problem in communication.

H) This is great! And it will also allow us to solve all owl-related issues. One just needs to have its own single-photon source and then quantum mechanics certifies communication security.

S) Uhm… About that part…

H) Yes?

S) Well, the only problem of QKD, as of today, is that efficient single-photon sources simply do not exist.

H) But this is terrible! Does it mean that the BB84 protocol will remain just a fantasy?

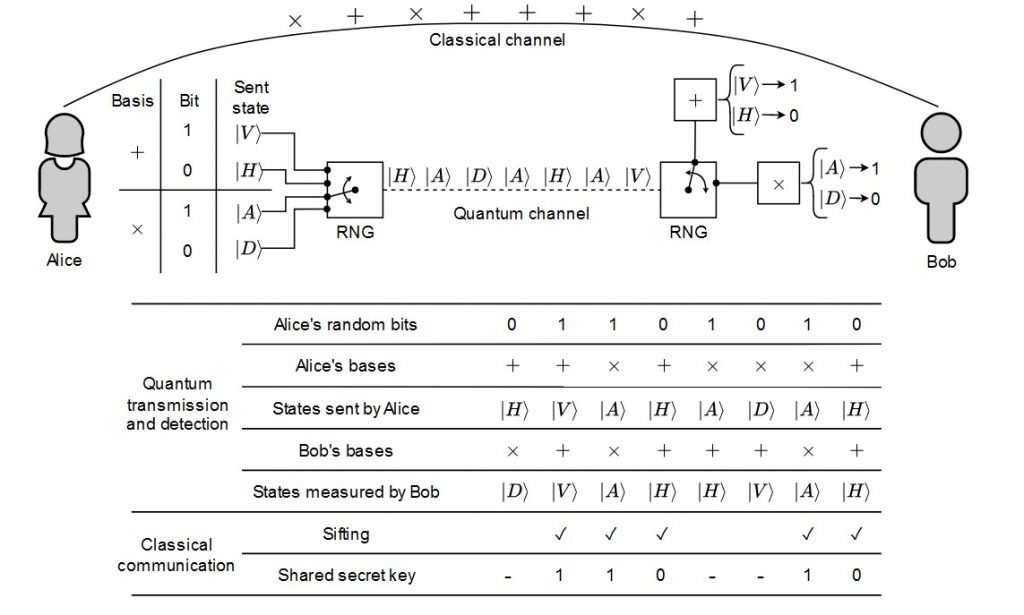
S) Oh no, we have other ways of making it work. You see, we want our QKD system to be as easy as possible to coexists with current telecommunication platforms. In practice, people use commercial lasers to create short light pulses. By performing what is called ”phase randomisation” of the laser pulses, we can theoretically prove that the content of each pulse is a certain number of coherent photons. The probability of having photons in a pulse is given by a Poissonian distribution P_µ(n) of mean µ, being µ the intensity of our laser. By tuning the intensity we can ensure that in the vast majority of cases our laser behaves as a single-photon source.

H) This is great! But I am worried… isn’t it a problem that some pulses have more than a photon?

S) Indeed, your instinct is correct. You see, the security of QKD relies on the fact that in quantum mechanics it is impossible to copy a certain quantum state. Hence, if an eavesdropper was to try to learn something about the single photon we are sending, he could not simply replicate it as he might do with classical bits. He will have to disturb it, and this contamination will alert us of his presence. However, if we were to produce multiple photons at once and encode information in all of them identically (as it would happen using polarization), then our enemy VoldEvemort could just take one of them, store it until we announce the basis we used and finally perform the same measurement operations.

H) But this would mean that every time we send a multi-photon pulse VoldEvemort will get all the information we are sending!

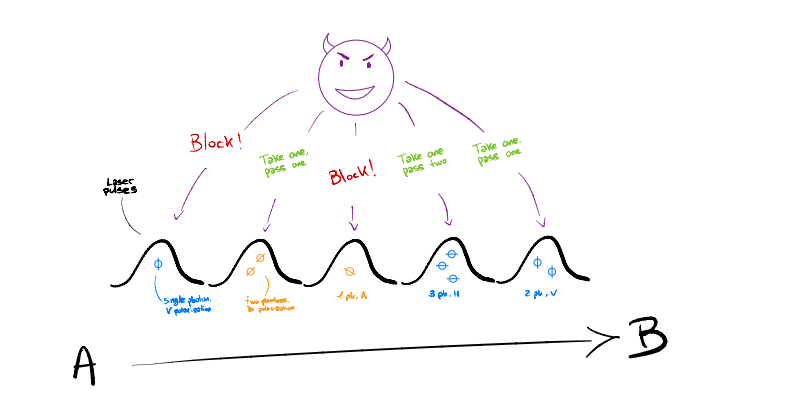
S) Exactly. And it doesn’t end here. In practice, we must design a channel for our travelling photons. These channels are of course realistic devices such as optical fibers or satellite links, which suffer from imperfections and, in particular, losses. It is not rare that some of the signals sent do not arrive at destination. Therefore, VoldEvemort could disguise himself as channel losses and proceed with the so-called Photon-Number-Splitting (PNS) attack. It works as follows: every time a single-photon pulse is sent, he blocks it and pretends it is a channel loss; every time a multi-photon pulse is sent, he just takes a photon and lets the rest of the light pass through. This would eventually result in him learning the 100% of the key without us noticing!

Professor Scrödingdore sketches something on the blackboard, you can find his drawings in figure 1.

Figure 1: Prof. Scrödingdore sketch of the PNS attack. Single-photon pulses are blocked, while multi-photon pulses are transmitted after storing one photon for further analysis.

H) This doesn’t sound good at all. It feels like if we produce multi-photon pulses there is no way to ensure security…

S) This was true until some years ago. Fortunately, we can now rely on the powerful Decoy State QKD technique.

H) Decoys? Like fishing ones?

S) The idea is similar. As I mentioned before, the best strategy for our enemy is to let all the multi-photon pulses pass and block all single-photon events. Talking mathematicsese, if we denote with Y_n the probability that a n−photon pulse emitted at the source is detected after the channel, then VoldEvemort’s actions lead to:

Y₁ = 0%
Y₂ = 100%, Y₃ = 100%, Y₄ = 100%, . . .

Note that with practical detectors we have no way of telling how many photon arrived, we can just discriminate between something and nothing. Of course, if VoldEvemort is not eavesdropping and we are dealing with a normal channel.

There would be no reason to have Y₁ = 0 and Y_≥2 = 1, as each photon will have a certain probability of arriving at the detector or be lost in the channel. Hence, if we manage to estimate these probabilities {Y_n}_n we can successfully detect the attacker’s presence and bound the amount of information he has learned.

H) This is interesting… I see potential in this idea, but I am still missing how we can implement it.

S) Very well. Let us be thinking out loud as a certain British songwriter.

Professor Scrödingdore modifies the sketches on the blackboard, see figure 2.

S) What would happen if we were to send on purpose some two-photon states and monitor how many of them are detected?

H) Well, if VoldEvemort wants to perform a PNS attack, he would have to take a photon for himself and let the other photon pass…

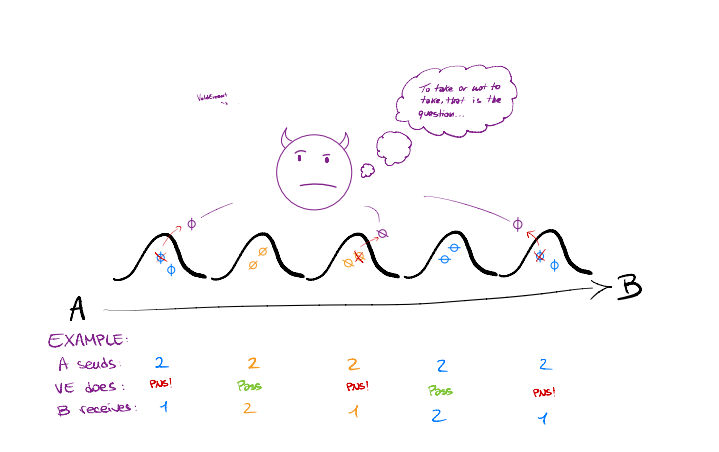
Figure 2: Prof. Scrödingdore sketch of the Decoy State method. If we send multiple decoys with two photons, the eavesdropper must choose between taking the photons (PNS attack, resulting in detection) or let the pulse go through (giving up on information).

S) Correct! But in this case we would always receive something and immediately know he is eavesdropping! Now, consider the following case: we will send each time either a signal or a decoy state. The former is a phase-randomised laser pulse containing a certain amount of photons, according to a Poissonian distribution with parameter µsignal. These photons are the ones we encode information in to generate key. The decoys are instead simple two-photon pulses. When VoldEvemort encounters a two-photon pulse, he cannot tell if it is a decoy or a signal with more than a photon, so his attack (and particularly Y₂) cannot depend on the type of state. This limits the power of his attack: by looking at what happens when we send a decoy state, we can learn the details of his attack on the signals!

H) This sounds like a great idea! So, how do we do this in practice? Preparing a perfect two-photon pulse will be very difficult in reality. To take or not to VoldEremort take, that is the question.

S) Indeed, this is true. Nevertheless, we can prepare multiple decoys in the form of phase-randomised pulses having different intensities ν₁, ν₂, . . . ν_n. All pulses will contain, with different probabilities, multiple photons. VoldEvemort only sees the photons without knowing the intensity used for preparation, which is instead known by the sender. By looking at the statistics of the detections upon sending various decoys, we can use a little algebra to estimate Y₂ (and any other Y_n). This eventually allows us to determine the amount of single-photon pulses that reach the detector, and therefore the security of our implementation. One of my more brilliant ideas and, between you and me, that’s saying something (Professor Scrödingdore smirks).

H) Wonderful Professor! Thank you a lot for the explanation. Although, I still have one last question: what is the impact of this new technique?

S) Oh it is enormous! You see Harry, until this point we were facing a quite unusual situation. For many years, the performances of experimental QKD have been simply much better than what the theory could justify. The reason for it is that when it comes to security we always consider the worst case scenario: as in every battle, we prefer to guarantee that we can provide limited safety against an exceptionally powerful adversary, rather than excellent security underestimating our opponent’s skills. Here we make no exception: if VoldEvemort is incredibly powerful, we must assume that he can learn every key bit we encode in a multi-photon pulse thought the PNS attack. In this case, we are only able to generate a secret key if the amount of single-photon states that reach the detector are more than the multi-photon states that our laser has sent. This would ensure that at least one single-photon state completed the transmission. In practice, we measure the performance of QKD by computing the Secret Key Rate (SKR), i.e. the amount of secret bits per second that we are able to share at a distance.

Professor Scrödingdore reminds Harry that he should definitely learn more about the SKR in the next story of the month: January 2024.

S) Experiments have shown that the SKR R is proportional to the channel transmittance η, which is defined as the percentage of bits per second that reach the detector (R ∝ O(η)). Nevertheless, theory had never been able to guarantee security better than R O(η²), which was seriously limiting the applications of QKD. This until the decoy state technique was introduced: it has been proven that with this tool R = O(η) holds also theoretically. This is a great step, as it allows to ensure communications at larger distances. This can be clearly seen in this painting…

Professor Scrödingdore magically turns the blackboard into a high-tech OLED display, portraying the plot you can find in figure 3.

S) In this figure you can look at how the performances of Decoy State QKD (in green) compare to the very same protocol without decoy (red line) and the theoretical case of perfect single-photon sources (blue). We notice that the linear part of the green and blue curves is the same (R O(η)) while the red decays faster (R ∝ O(η²)). Moreover, the maximum reachable distance is also much greater, approaching the ideal single-photon case. This is the impact of Decoy State QKD!

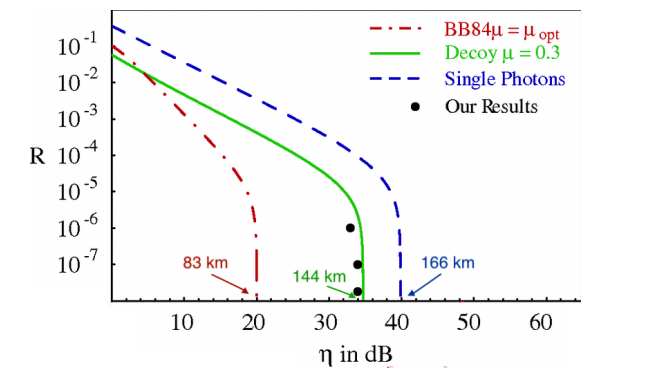
Figure 3: Secret Key Rate (R) as a function of the transmittance η. SchmittManderbach T., et al. ”Experimental Demonstration of Free-Space Decoy-State Quantum Key Distribution over 144 km”.

H) This is fabulous Professor! Thanks a lot for your explanations!

S) Is my pleasure, dear Harry. But now, might I ask your help with a fundamental question that has been bugging me quite a lot recently?

H) Of course Professor! What is it about?

S) You see that box over there? I put a cat in it some time ago, but now I can no longer tell whether it is dead or alive…

Note of the Author:

In this Story of the Month I cared to present, in a playful way, a cornerstone result of modern implementations of Quantum Key Distribution systems. It is for me important to stress how the idea that I didactically depicted in here is the original one, while the past decades led to an evolution of it. In today’s experiments, all the pulses emitted by Alice are indeed phase randomised pulses of various weak intensities (namely, a signal one µ_signal and one or more decoys {ν_n}_n ). The best security proofs of QKD with decoy states are based on the fact that different source intensities imply a different amount of expected detections after the channel. By analysing the latter data, we can eventually bound the amount of key bits we have to sacrifice for privacy amplification and determine the secret key rate. My current research takes place exactly in the domain of security proofs of QKD, treating this and other implementation flaws that undermine the practical realisations of this technology.

The original Decoy State idea:

Hwang, W.-Y. ”Quantum Key Distribution with High Loss: Toward Global Secure Communication”. Phys. Rev. Lett. 91 (5): 057901 (2003)

More on the topic:

Lo H.-K., et al. ”Decoy State Quantum Key Distribution”, Phys. Rev. Lett. 94, 230504 (2005).

Lim C., et al. ”Concise security bounds for practical decoy-state quantum key distribution”, Phys. Rev. A 89, 022307 (2014).