Memory-Hard hash functions.

Apr 2025

Gina Muuss

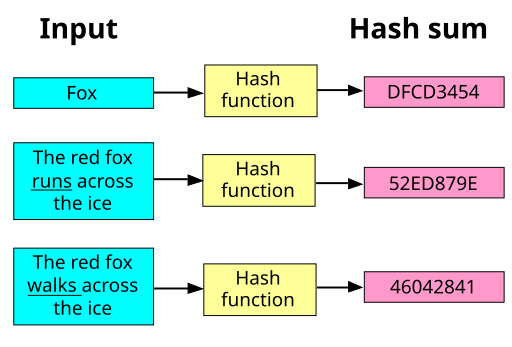
Memory-Hard hash functions are a cryptographic primitive used to make hash functions more expensive to implement in hardware. This reduces the financial efficiency of ASIC based brute-force attacks. Examples used in industry are Argon2 and scrypt.
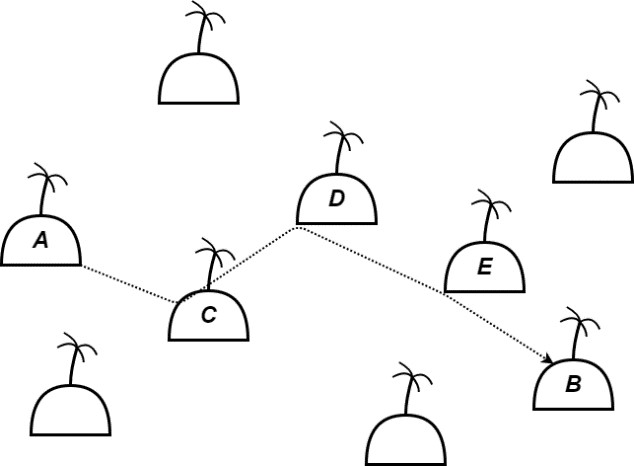
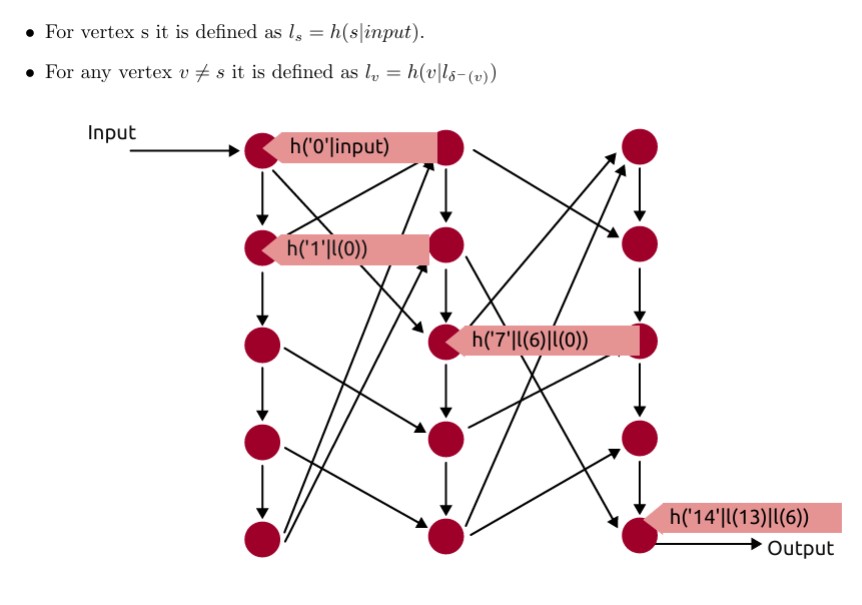
To construct the memory-hard function a normal cryptographic hash function h is used. Additionally, a graph G with vertices V is picked. We call the vertices with edges to a vertex v its parents δ−(v). There is one exception to this rule, a vertex we call s, the start vertex. We also name one other vertex t, the target vertex. To compute the value of the function we need to compute the label of vertex t. The label of a vertex is defined recursively as follows (| denotes string concatenation):

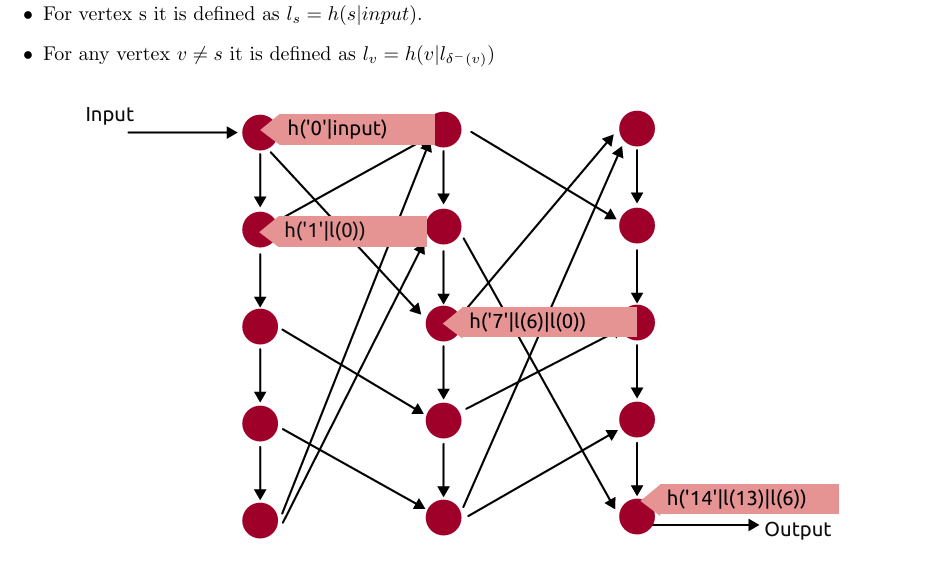
Figure 1: An example graph with exemplary labels for some nodes.

You can also see this in Figure 1, the graph is effectively our data-dependency graph, and we compute the final note at the bottom right. It is an open question in computer science how much memory is required to classically compute the value of this function with respect to the graph chosen. It is also an open question in (post)-quantum cryptography.