Latticia and the Web of Trapdoors.

May 2025

Fabrizio Sisinni

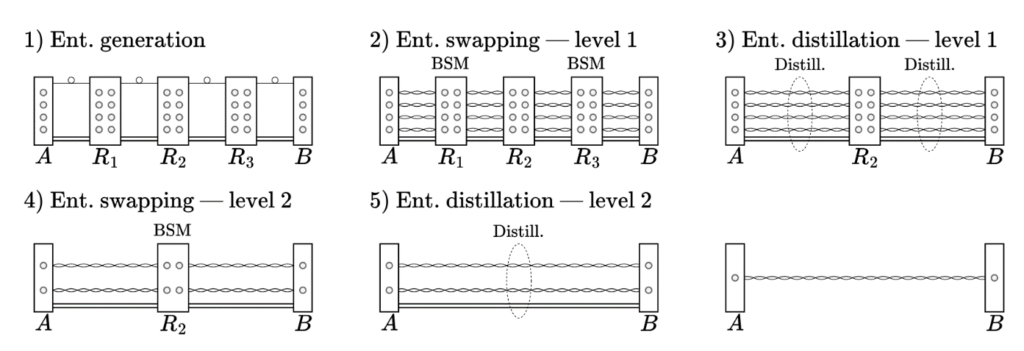
In the land of Cryptonia, spiderwebs were more than homes—they were mathematical puzzles. Each web was built on a hidden structure called a lattice; a network of strong, stable points connected by threads. These special points formed the skeleton of the web, and moving between them required a set of instructions: a basis, a list of moves that could take a spider from one safe point to another.

Young Latticia was the daughter of Mathema, the greatest cryptographic web-spinner in all of Cryptonia. One morning, Mathema gathered Latticia and her two brothers in the heart of her shimmering web. “Today,” she said, “you will face three challenges. Each will test how well you understand the secrets of the web. I’ve given each of you a different basis to move across it. Latticia, yours is short and elegant. Yours,” she told her sons, “are… more tangled.”

The web was the same for all—but the tools were not.

Challenge 1: The Shortest Safe Path (SVP – Shortest Vector Problem)

Mathema pointed to the center of the web.

“Your first task is to find the shortest safe route from here to any other stable point in the web. This is the secret to building strong silk and moving quickly.”

Latticia looked at her basis—the short, straight moves—and spotted the closest stable point in no time. She zipped across the web with ease.

Her brothers squinted and scurried, using their long, twisted steps. Their paths were confusing, and it took them much longer to find the same point.

“In lattices, we call this the Shortest Vector Problem,” Mathema explained. “It’s easy when you have a good basis—almost impossible when you don’t.”

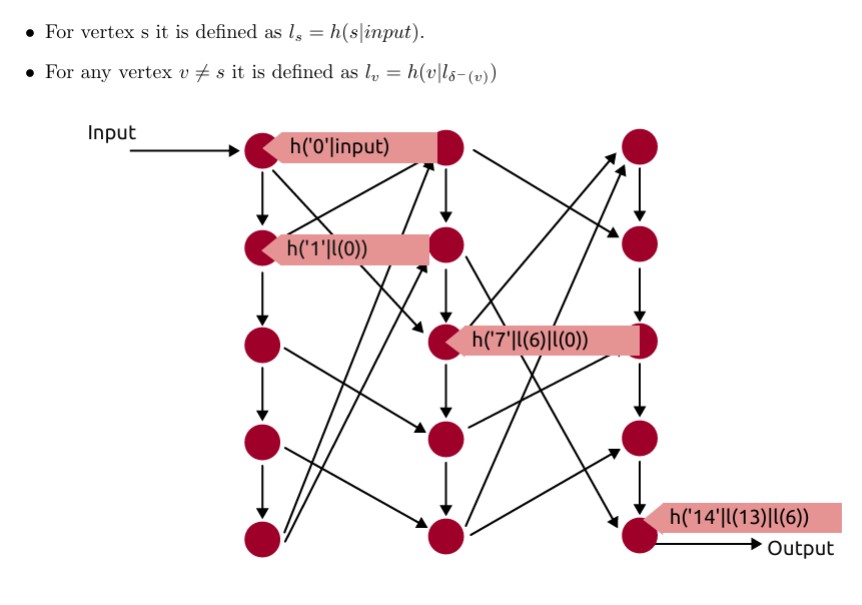
Challenge 2: The Nearest Hunting Spot (CVP – Closest Vector Problem)

For the next task, Mathema dropped a small insect onto a random spot on the web—not on a lattice point.

“Now,” she said, “find the nearest safe point to this prey. That’s where you’ll want to strike from. But remember—you’re not standing at a lattice point anymore. You must search for the closest one.”

This was harder. The insect didn’t sit directly on a known anchor point, and only by understanding the web’s structure could the spiders choose the best position to pounce.

Again, Latticia used her neat, compact basis and found the nearest safe anchor quickly. Her brothers zigzagged, overshot, and circled around, missing their targets.

“This is the Closest Vector Problem,” said Mathema. “In real cryptography, this is how we decode messages. But without the right basis—without the trapdoor—it’s just guessing in the dark.”

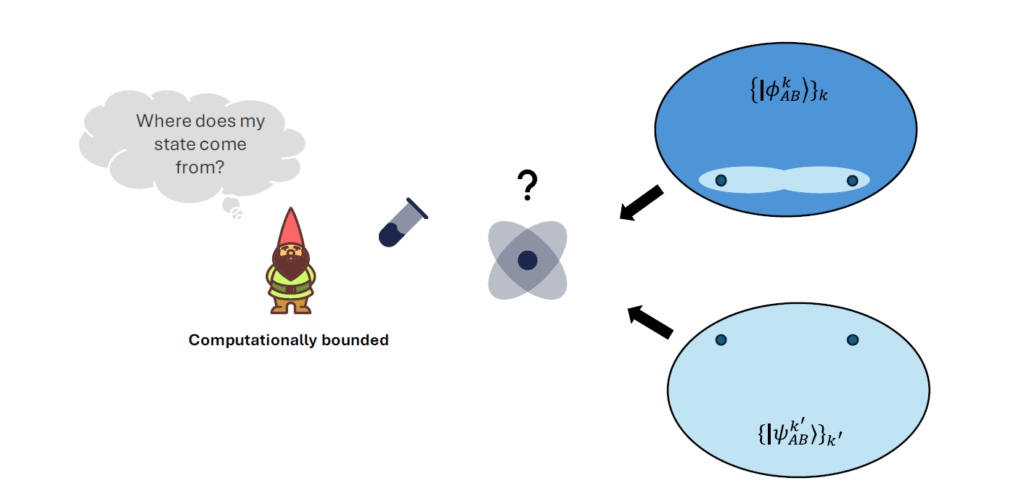
Challenge 3: The Fuzzy Instructions (LWE – Learning With Errors)

For the final challenge, Mathema lowered three scrolls of silk, each one filled with strange, noisy instructions.

“These scrolls tell you where I’ve hidden a treasure. But I’ve scrambled the clues—each one is a bit fuzzy. Your job is to understand the noise, and find the treasure anyway.”

Her sons tried their best, reading and re-reading the scrolls, but the noise confused them. The clues seemed to contradict each other.

Latticia, on the other hand, used her knowledge of the web and her clean basis—the trapdoor—to cut through the fuzz. She could see what the clues should have been, and pieced together the hidden location.

“This is the heart of the Learning With Errors problem,” Mathema said. “We hide secrets in fuzz, so that only those with the right moves can make sense of the message.”

The Cryptographer’s Path

Latticia had passed all three challenges. She learned that having the right view of the web—the right basis—could make hard problems simple. And she saw how this secret could protect information from even the cleverest invaders, including the feared quantum eagles that could tear through ordinary cryptography.

From that day on, Latticia trained not just as a spider, but as a cryptographer, ready to spin webs that were strong, smart, and secure.