Just Guess! Improved Algorithm for underdetermined MQ solving

Jul 2025

Massimo Ostuzzi

In this story of the month, we dive deep into the world of cryptographic signature schemes and their security.

What’s the Big Deal About MQ Problems?
At the heart of our story is the Multivariate Quadratic (MQ) problem. Think of it as solving a bunch of messy equations where every variable is multiplied by another at most once and one has to find an assignment for these variables that satisfies all equations simultaneously. These puzzles are tricky—so tricky, in fact, that many post-quantum digital signature systems rely on their hardness to stay secure. Systems like MAYO, QR-UOV, and SNOVA all use this math to protect digital signatures. Cracking their underlying equations would mean forging someone’s digital signature—meaning troubles security-wise, as you could impersonate somebody else, or vice versa. Figuring out the limits of such systems is key to keeping future technology safe.

The Challenge: Underdetermined Systems
In these schemes, there are usually more variables than equations, that’s why we call them “underdetermined” MQ system. This means that there are multiple solutions to the problem! Previous approaches either tried to solve the whole system directly (which gets complex fast) or simplified parts of it. The best-known algorithm until now was by Hashimoto, which cleverly splits the problem into two
smaller chunks.

Our Idea: More Blocks
We thought, “Why just two blocks? Why not more?” So we developed a multi-block approach that breaks the problem into several bite-sized pieces. It’s like organizing a big puzzle into manageable sections instead of trying to finish it all at once.

This shift brought several cool benefits:
– Smaller MQ subproblems: Easier and quicker to solve.
– Less memory usage: Great for actual implementation.
– Better fit for parallel computing: Many small problems can be solved at the same time.
– More reliance on guessing: That might sound bad, but guess what? It actually makes the problem more vulnerable to quantum attacks!

Just Guess
Our method leans more on guessing parts of the solution and then solving very tiny systems to check if the guess was right. This turns out to be great for real-world applications and even opens the door to powerful quantum attacks using Grover’s algorithm (which speeds up guessing).

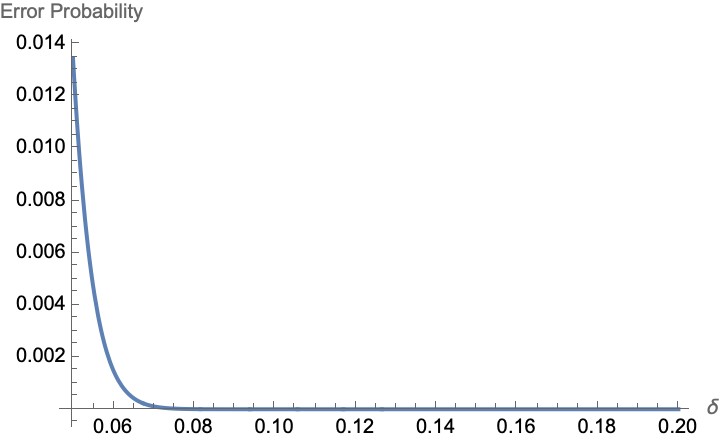
Real Impact: Cutting Down Security Bits
When we tested our method on signature the schemes MAYO, QR-UOV and SNOVA, we managed to reduce the classical security by a big margin for many proposed parameter sets and the quantum security for all proposed parameter sets. In particular, the more underdetermined the underlying MQ problem is, the better our algorithm performs. We also have a parameter, called underdeterminedness ratio, that can give hints about the performance of our algorithm for given parameter. Moreover, our approach also benefits when the underlying finite field is relatively small, since this makes the guessing cheaper! In practical terms, our approach makes some of today’s “safe” schemes look a bit more fragile than previously thought.

Final Thoughts
Breaking things isn’t always bad: in cryptography, that’s how we learn to build them better. Our goal isn’t to enable malicious forgery, but rather to help strengthen future digital signature schemes. We hope our result inspires new, more secure designs in the post-quantum world.