Beyond Polls: Concentration Inequalities in Quantum Key Distribution.

Oct 2024

Vaisakh Mannalath

In my previous story of the month, I discussed concentration inequalities and their everyday applications, such as election polling. This month, I’ll dive into their relevance in my research, focusing on improving the efficiency of Quantum Key Distribution (QKD) protocols.

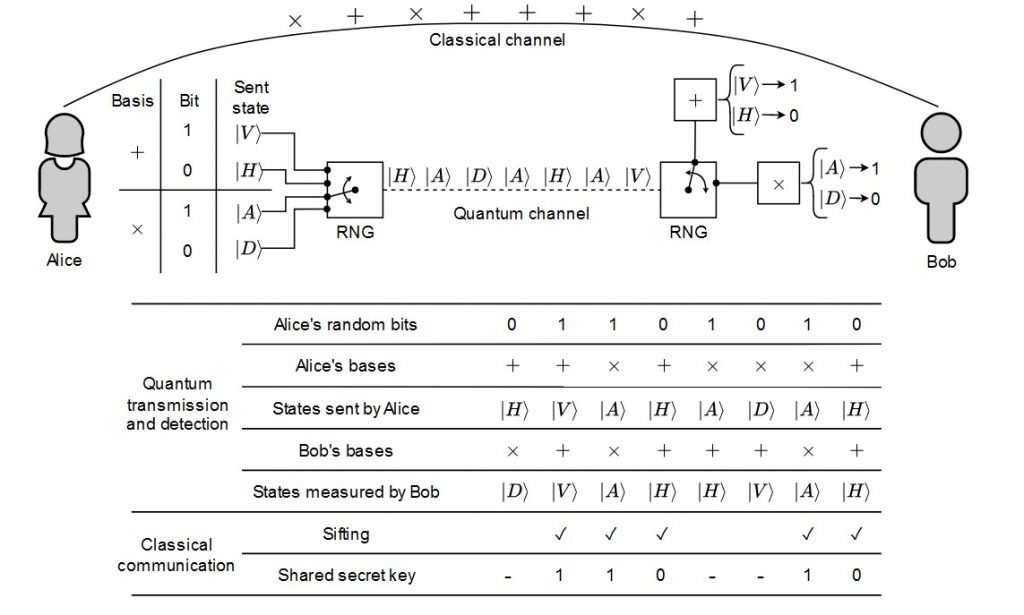
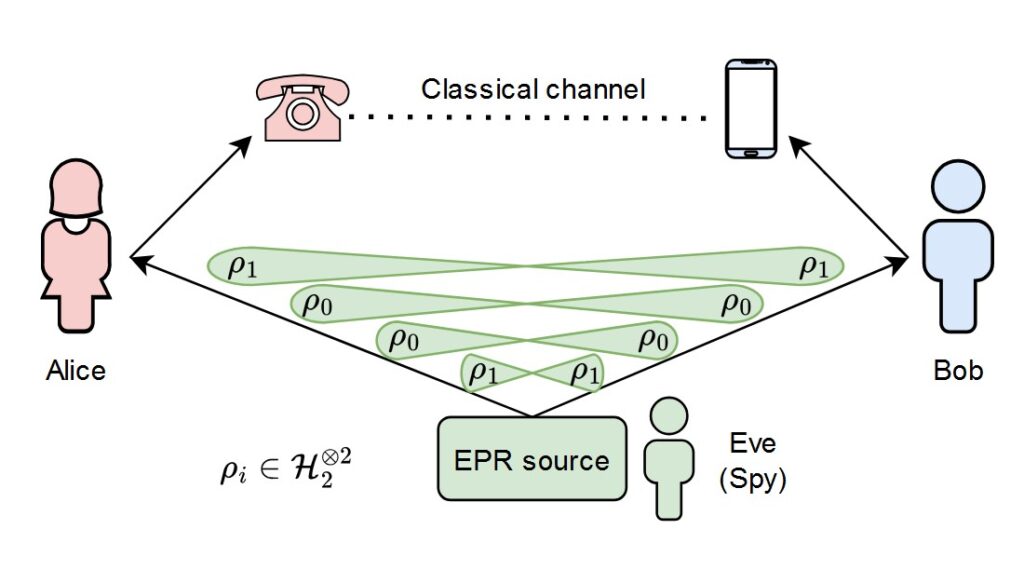
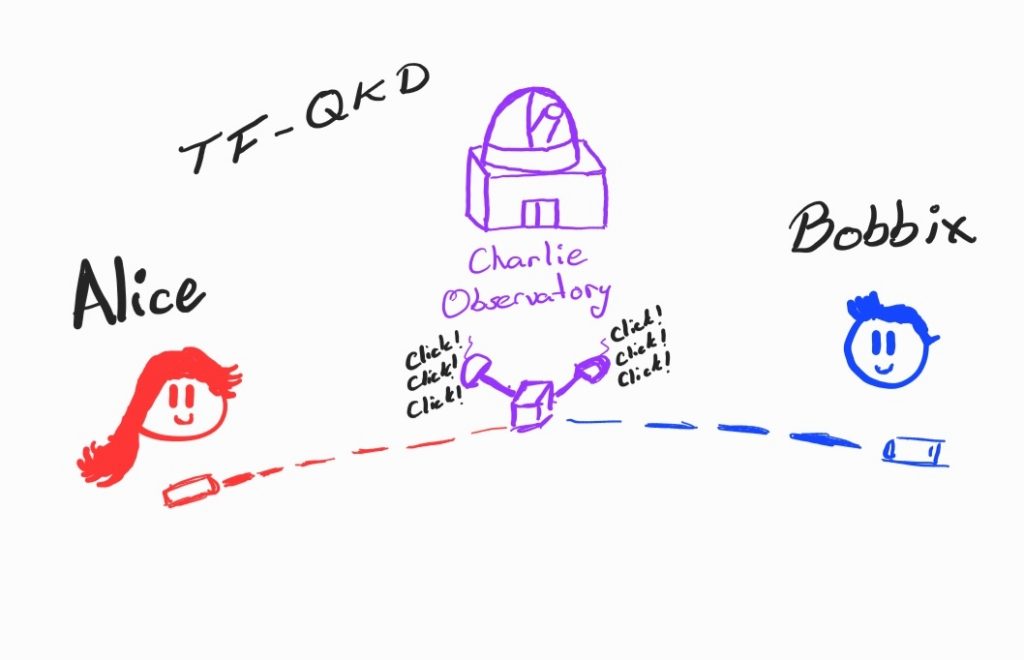
The goal of a QKD protocol is to establish a shared, provably secure secret key between two parties, using photons for key transmission. However, environmental factors can introduce errors in photon transmission, which must be estimated as part of QKD’s security analysis. This is where concentration inequalities play a crucial role.

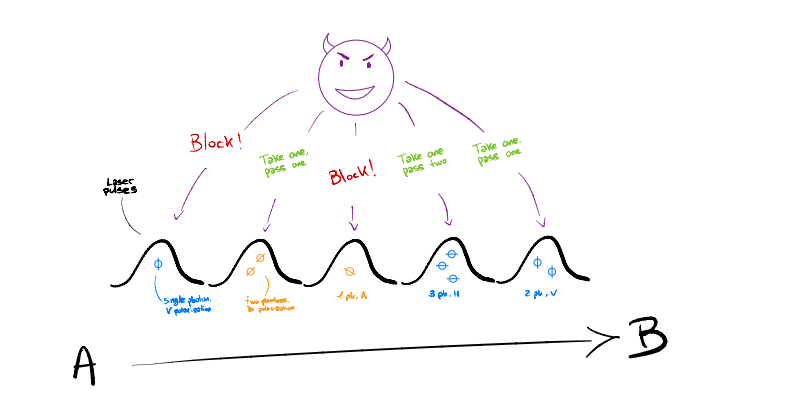
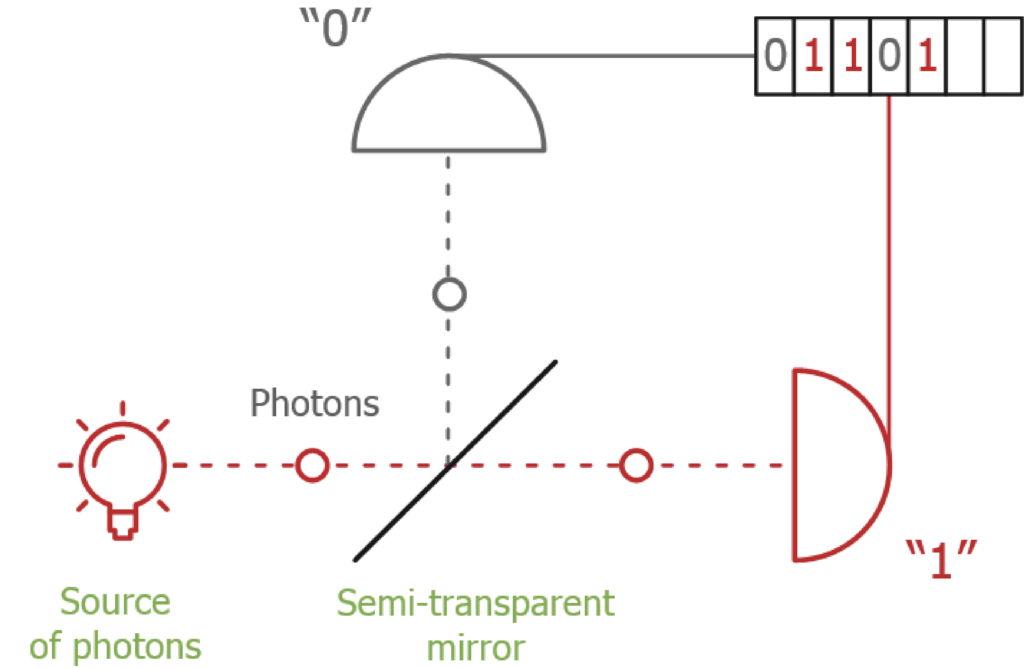
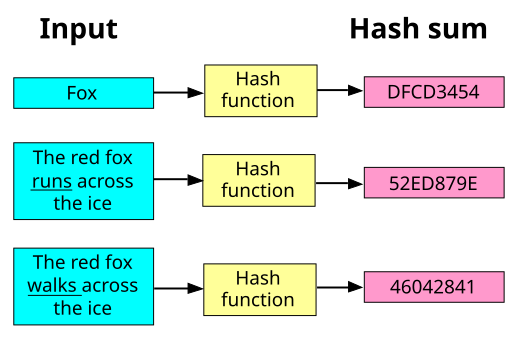
The part of the QKD protocol where error rates are estimated is called parameter estimation. At this point, the parties have a set of photon detections and sample a subset randomly for error testing. The error rate in this test set, denoted by p, is publicly revealed. A video below summarizes these steps, with green circles representing correct detections and red indicating errors and blue boxes denoting the random sampling. The key set’s error rate, q, remains unknown and cannot be observed directly, with the distribution of errors remaining uncertain.

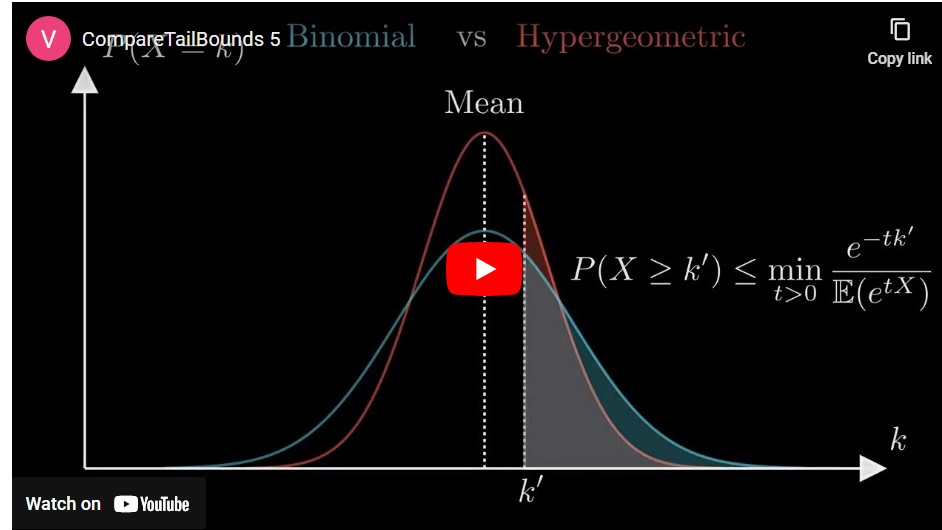
This is where concentration inequalities come into play. Although q is a random variable, we know it belongs to a certain distribution. Specifically, the random sampling ensures that both the test and key sets follow a hypergeometric distribution, with the mean reflecting the total error rate.

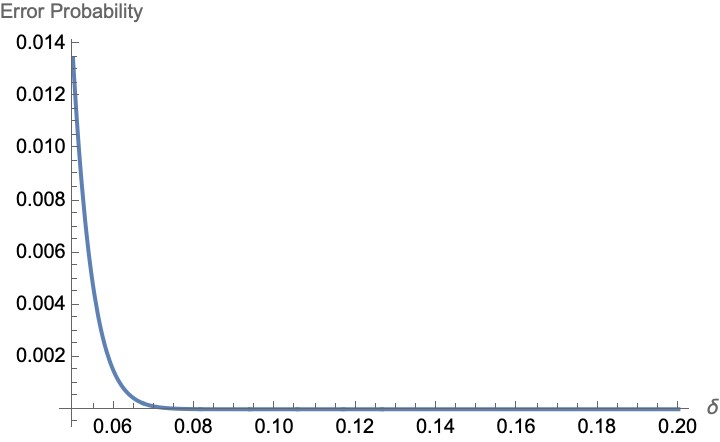
By leveraging this distribution, we can bound the error rate in the key set using probability theory. We’re particularly interested in an upper bound, as it ensures a worst-case scenario for QKD performance. However, we can’t make exact predictions—so we calculate the probability that the error rate exceeds this upper bound. If this probability is small, the bound is highly reliable. These probabilities, called tail inequalities, can’t be calculated directly for QKD due to large numbers involved, so we rely on looser bounds, often starting with the Markov Inequality. Markov’s inequality is only the beginning, though—we need to simplify it further to get usable bounds.

Traditionally, these loose bounds for hypergeometric distributions have been used in QKD error rate estimation. However, we found a more efficient approach. Notably, we observed that the binomial distribution’s tail probabilities can be used to bound those of the hypergeometric distribution, based on a result from [Hoeffding 1974].

While binomial-based bounds might seem less tight under Markov’s inequality, we discovered that in the context of QKD, this approach offers significant advantages. By replacing traditional methods with our new bounds, we reduced QKD protocol requirements by 16%-25% and improved security by two orders of magnitude! This improvement could greatly enhance the performance of practical QKD protocols, including satellite-based QKD.