STORY OF THE MONTH
Understanding Provable Security: The Foundation of Trust in Cryptography
 Oct 2025
Oct 2025  Silvia Ritsch
Silvia Ritsch
In the ever-evolving world of cryptography, trust is everything. When we rely on encryption protocols to safeguard our data, we need to be confident that they actually work. This is where provable security comes into play. But what does it mean to have “provable security”? And why is it essential for building secure systems? Let’s dive in.
What is Provable Security?
Provable security is a concept in cryptography that aims to offer mathematical guarantees about the security of cryptographic algorithms. Unlike empirical security, which relies on testing and heuristics, provable security provides rigorous proofs that a system is secure under certain assumptions.
In simple terms, it means demonstrating that breaking a cryptographic protocol is computationally infeasible, assuming certain conditions (or hardness assumptions) hold. These proofs often take the form of mathematical reductions, where breaking the security of a protocol is reduced to solving a problem that is known to be hard.
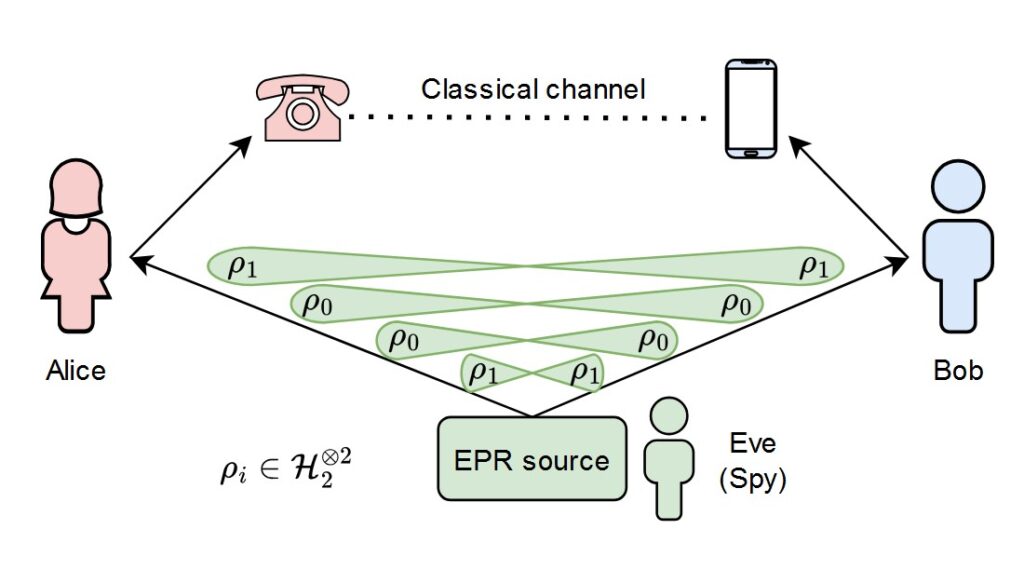
For example, the security of RSA encryption is often based on the assumption that factoring large composite numbers is computationally infeasible. If this assumption holds, the RSA algorithm remains secure. If an attacker could factor large numbers quickly, RSA would be compromised.
Why is Provable Security Important?
In a world where cyber threats are rampant and evolving, we need more than just “it works” when it comes to cryptography. Provable security offers a level of certainty and confidence that is crucial for real-world applications. Here’s why it matters:
1. Mathematical Assurance
Provable security provides mathematical certainty that cryptographic protocols are secure against known attacks. Unlike empirical security, which can only test a system against known adversarial strategies, provable security allows cryptographers to demonstrate that certain attacks are computationally impractical, no matter how powerful the attacker is.
2. Reductionist Approach
In provable security, protocols are typically analyzed through reductions. This means that a cryptographic problem is shown to be at least as hard as another well-studied problem (like integer factorization or discrete logarithms). If the harder problem is assumed to be difficult (i.e., no efficient algorithm exists), then the cryptographic protocol is secure under that assumption. This makes it easier to trust the security guarantees because of the logical reasoning behind them.
3. Resilience Against New Attacks
The formal nature of provable security helps anticipate and defend against future attack vectors. If a new type of attack emerges, it can be incorporated into existing models, and the security of protocols can be reassessed. This dynamic nature allows cryptography to adapt to new challenges in the cyber landscape.
4. Confidence in Protocols
When a cryptographic protocol has been proven secure, it is much easier to adopt it in real-world applications. For example, many widely used protocols like TLS (used in HTTPS) rely on provable security for their integrity. Users can trust that their communications are safe because experts have rigorously proven that breaking the encryption is infeasible, assuming the cryptographic assumptions hold true.
The Foundations of Provable Security
The backbone of provable security rests on two critical elements: hardness assumptions and security models.
1. Hardness Assumptions
Hardness assumptions are the mathematical problems that cryptographic protocols are based on. For instance, RSA’s security is tied to the difficulty of factoring large numbers, while the security of elliptic curve cryptography (ECC) depends on the difficulty of the Elliptic Curve Discrete Logarithm Problem (ECDLP). These problems are assumed to be computationally hard, meaning no efficient algorithms exist to solve them in a reasonable amount of time.
If the hardness assumption of a protocol is broken (say, someone develops an efficient factoring algorithm), the protocol’s security can no longer be guaranteed. This highlights the importance of constantly reassessing and verifying the validity of hardness assumptions.
2. Security Models
In provable security, cryptographic systems are analyzed within a specific security model. This model defines the adversary’s capabilities, including the types of attacks they can mount and the resources available to them. Common models include:
The Random Oracle Model (ROM): This model assumes an idealized function (like a hash function) that behaves randomly but deterministically when queried. Many proofs of security are conducted within the ROM, as it simplifies analysis.
The Standard Model: This model works with more realistic assumptions about real-world functions and protocols, making it more applicable in practical settings, but often harder to prove security.
Security models help in assessing the strengths and weaknesses of cryptographic systems in different contexts. A protocol might be secure in one model but vulnerable in another, depending on the assumptions made about the adversary’s capabilities.
Challenges and Limitations
While provable security offers powerful guarantees, it’s not without its challenges and limitations:
Assumption Dependence: The security of many protocols hinges on assumptions about the hardness of specific problems (e.g., factoring or discrete logarithms). If these assumptions are proven false or weakened, the security of the entire system could be compromised.
Complexity: Writing a formal security proof is often a highly complex and time-consuming process. For newer protocols, it might take years of academic research to rigorously prove their security, especially in the face of evolving attack methods.
Idealized Models: Many proofs are conducted in idealized models (such as the Random Oracle Model) that do not necessarily reflect real-world conditions. As a result, a protocol might be provably secure in one model but fall short when implemented under real-world conditions.
Quantum Threats: The rise of quantum computing poses a significant challenge to classical cryptographic assumptions. Problems that are currently believed to be hard, such as factoring large numbers, may become easy with quantum algorithms (e.g., Shor’s algorithm). As a result, the field of post-quantum cryptography is emerging to develop new protocols that are resistant to quantum attacks.
The Future of Provable Security
As we continue to rely on cryptographic protocols for securing everything from online banking to private communications, the need for provable security is becoming even more critical. The shift toward quantum-resistant algorithms, the rise of new attack strategies, and the increasing complexity of cryptographic systems will drive the development of more advanced proof techniques and models.
In the near future, provable security will not only help ensure the safety of digital systems but will also be essential for establishing trust in emerging technologies such as blockchain, AI-powered cryptography, and secure multi-party computations.
Conclusion
Provable security is a cornerstone of modern cryptography, offering mathematical assurance that our digital systems can withstand malicious attacks. By building cryptographic protocols on well-defined hardness assumptions and formal models, we can create systems that are not only secure but also resilient to new and unforeseen threats. As technology advances, the role of provable security in safeguarding our digital lives will only grow more important, ensuring that trust in the cryptographic systems that underpin the modern world is well-placed.
In a nutshell, provable security provides us with the confidence to trust our online systems and communications. But like any powerful tool, it requires constant attention, careful analysis, and evolution as new challenges arise.
OTHER STORIES